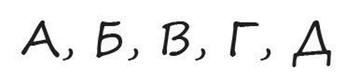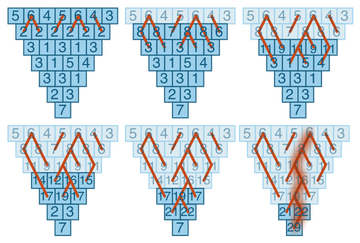Задача №1.
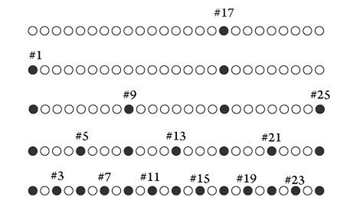
На доске записаны числа, вам нужно ответить на вопрос: какое число идёт дальше?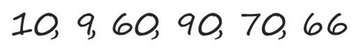
Чаще всего все пытаются отыскать – безуспешно – какую-либо закономерность в серии чисел, которая кажется совершенно бессмысленной. Но здесь нужно забыть математику. Произнесите эти числа на английском (см. рисунок), окажется, что они расположены в порядке возрастания числа букв, содержащихся в их написании.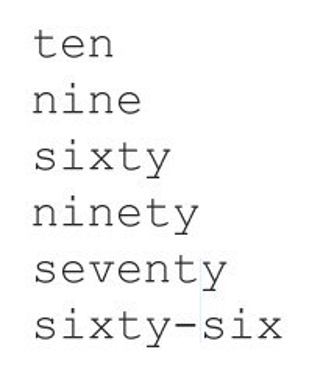
Теперь приглядитесь еще более внимательно к этой серии. 10 – не единственное число из трёх букв. На этом месте могло бы быть 1, 2 и 6 (one, two и six). То же можно сказать и про 9, подойдут 0, 4 и 5 (zero, four и five). Таким образом можно сделать вывод, что в список включены самые крупные числа из тех, что можно выразить словами с заданным числом букв.
Так какой будет правильный ответ? Очевидно, что в числе, следующем за 66, должно быть девять букв (не считая возможного дефиса), и оно должно быть самым крупным в своём роде. Немного подумав, можно сказать, что ответ будет 96 (ninety-six). Вы понимаете, что сюда не подходят числа, превышающие 100, поскольку для «one hundred» уже нужно десять букв.
Может быть, у вас возникнет вопрос, почему в приведённом списке на месте 70 не стоит сто (hundred), или миллион, или миллиард, для написания которых также нужно семь букв. Скорее всего потому, что на правильном английском языке говорится не «сто», а «одна сотня», то же относится и к двум другим случаям.
Казалось бы, всё, вот он правильный ответ. В Google его считают приемлемым, но не самым совершенным. Есть число побольше:
10 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000,
которое записывается как «one googol» (девять букв).
Однако и это еще не самый лучший вариант. Идеальный ответ: «ten googol», десять гуголов.
Задача №2.
Задача, которая была популярна в своё время на собеседованиях в Amazon. Мы русифицировали её, но смысл остался тот же. Вам нужно продолжить последовательность.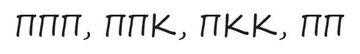
Вот один из возможных ответов на эту задачу. Последовательности сопоставлены буквы алфавита, закодированные в набор «П» и «К» — некоторых характеристик. Нужно найти что-то, чего в букве А три, в Б — две и т.д. Тут подходит количество прямых штрихов и кривых. Далее несложно догадаться, что букве Д соответствует, например, «ППППП», в случае её написания как на предложенном рисунке.
Последовательности сопоставлены буквы алфавита, закодированные в набор «П» и «К» — некоторых характеристик. Нужно найти что-то, чего в букве А три, в Б — две и т.д. Тут подходит количество прямых штрихов и кривых. Далее несложно догадаться, что букве Д соответствует, например, «ППППП», в случае её написания как на предложенном рисунке.
Идеи и решения от подписчиков
В комментариях к посту с задачей можно было найти множество интересных решений, которые перечислены ниже.
Алгоритмы Маркова
Оба алгоритма работают при проходе с конца строки.
{КК -> П; П -> К}
Ответ: ПК, КК, П, К
{ПП -> ПК; КК -> П}
Ответ: ПК
Двоичная система счисления
П — это 1, К — это 0.
Тогда закономерность в десятичной системе счисления будет иметь вид:
• 7 (ППП — 111),
• 6 (=7-1) (ППК — 110),
• 4 (=6-2) (ПКК — 100),
• 3 (=4-1) (ПП — 11),
а значит, далее следуют
• 1 (=3-2) (1 — П) и
• (=1-1) (0 — К).
Ответ: П, К.
Цикл
Существует цикл заполнения строки буквами К с конца, при этом, когда остается всего одна П (очевидно, слева), то вся строка преобразуется к строке из букв П, но на одну меньше, т.е.:
• ППП
заполняем буквами К с конца
• ППК
• ПКК
осталась одна П, уменьшим длину
• ПП
• ПК
снова укорачиваем
• П
Ответ: ПК, П
Скобочная последовательность
Забавный вариант: П — пусть, К — конец, тогда можно построить аналогию с открывающимися-закрывающимися скобками 🙂 Закономерность не найдена.
Онлайн-курсы Domestika
13 апреля – 1 июня, онлайн, беcплатно
tproger.ru
События и курсы на tproger.ru
UPD. Был предложен вариант рассматривать всю последовательность букв как единую скобочную последовательность:
• ((( (() ()) (( )) )))
ППП ППК ПКК ПП ККК КК
или
• ППП ППК ПКК ПП КК ККК
Ответ: ККККК (в разных вариантах: КК, ККК или ККК, КК и т.п.)
Несоставные числа
Посчитаем количество «дырок в буквах»:
• ППП — 3
• ППК — 5
• ПКК — 7
• ПП — 2
Заметим, что все это — простые (т.е. не составные) числа до 10. Заметим, что есть еще только одно не составное число, меньшее 10 — это единица.
Ответ: П
Произведение 1 и -1
П — это -1. К — это 1. Вариант наоборот, естественно, также подойдет. Тогда рассмотрим их произведения:
• ППП = -1
• ППК = 1
• ПКК = -1
• ПП = 1
вариантов продолжения несколько, автор предложил такой:
• ПК = -1
• КК = 1
• П = -1
• К = 1
Ответ: ПК, КК, П, К
Сумма
П = 15, К = 10. Естественно, подойдут любые другие числа такие, что П:К = 3:2. Рассмотрим ряд:
• ППП: П+П+П = 45
• ППК: П+П+К = 40
• ПКК: П+К+К = 35
• ПП = 30
в качестве продолжения напрашиваются:
• ПК = 25
• КК = 20
• П = 15* К = 10
Ответ: ПК, КК, П, К
Русский язык в помощь
Вариант с хронологией выпуска девайсов:
• ППП — первое промышленное производство, или первое производство процессоров
• ППК — первый персональный компьютер
• ПКК — первый карманный компьютер
• ПП — первый планшет
• ПС — первый смартфон
Ответ: ПС
Азбука Морзе
К сожалению, закономерности найти никто не смог. Может быть, это удастся вам?
Занимательно то, что при разных вариантах решения очень часто появлялся ответ ПК, КК, П, К…
Задача №3.
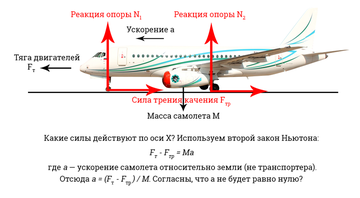
Здесь нужно отметить, что при ближайшем рассмотрении условие задачи оказывается некорректным. Во-первых, шасси вращаются с угловой скоростью, а лента с линейной, поэтому их сравнение некорректно. Во-вторых, если принять, что угловая скорость колес транспортера равна угловой скорости колес самолета и их диаметры равны, то задача сводится к неподвижному относительно земли самолету. Но будем исходить из того, что транспортер просто движется так, чтобы не дать едущему по транспортеру самолету перемещаться относительно земли. Конечно, с точки зрения физики задача не совсем корректна и по другим причинам, но попробуем решить ее эмпирически.
Большинству из нас сразу приходят на ум ассоциации с автомобилем, пытающимся разогнаться по транспортеру. Соответственно, очень многие обычно отвечают: нет, не взлетит. Но так ли это? Попробуем разобраться.
Сначала нужно вспомнить, почему вообще летает самолет. Двигается он под действием силы тяжести, силы тяги и подъемной силы. Всеми остальными силами можно пренебречь. Двигатели самолета создают тягу за счет отбрасывания воздуха или продуктов сгорания топлива. Сила тяги, преодолевая действие прочих сил (трения, сопротивления воздуха), придает самолету ускорение.
После включения двигателя скорость самолета относительно земли начинает возрастать. Кроме того, самолет начинает все меньше и меньше давить на ВПП из-за возникающей на крыльях за счет движения относительно воздуха подъемной силы. До тех пор, пока подъемная сила не станет равной силе тяжести, самолет давит на взлетную полосу. Как только скорость самолета относительно воздуха достигает определенной величины, подъемная сила начинает полностью уравновешивать силу тяжести. После чего самолет может взлететь.
«Но как же движение транспортера?» — спросите вы. — «Самолет ведь перед взлетом должен разогнаться, разве он сможет сделать это в таких условиях?»
Самолет взлетит только тогда, когда у него будет достаточная скорость относительно воздуха. Почему она появится? Потому что самолет отталкивается не от земли, а от воздуха. Это не автомобиль, который бы не сдвинулся с места в аналогичных условиях. Самолету все равно, что под ним — бетонная ВПП, движущаяся лента или лед.
Движение самой взлетной полосы при решении задачи несущественно. Даже оно не остановит самолет относительно наблюдателя, стоящего на земле — просто шасси будут вращаться вдвое быстрее, чем при неподвижном полотне. Аналогично можно показать, что любое движение взлетной полосы приводит лишь к изменению скорости вращения шасси самолета, но не влияет на движение самого самолета. Транспортером можно остановить вращение шасси, но не сам самолет. Сила трения вращения шасси пренебрежительно мала по сравнению с тягой двигателей и не способна помешать ему взлететь.
Задача №4.
В этом выпуске рассмотрим классическую задачу, известную под названием «Золотая гора». На CheckiO её реализовали в этой задаче.
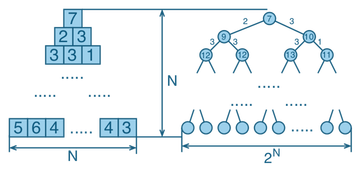
Представьте себе треугольник, составленный из чисел. Одно число расположено в вершине. Ниже размещено два числа, затем три, и так до нижней грани. Вы начинаете на вершине, и нужно спуститься к основанию треугольника. За каждый ход вы можете спуститься на один уровень и выбрать между двумя числами под текущей позицией. По ходу движения вы «собираете» и суммируете числа, которые проходите. Ваша цель – найти максимальную сумму, которую можно получить из различных маршрутов.
Рассмотрим различные методы решения.
Рекурсия
Первым делом в голову приходит мысль использовать рекурсию и просчитать все пути от вершины. Когда мы спускаемся на один уровень, то все доступные числа ниже образуют новый меньший треугольник, и можно запустить нашу функцию уже для нового подмножества и так пока не достигнем основания.
def golden_pyramid(triangle, row=0, column=0, total=0):
global count
count += 1
if row == len(triangle) - 1:
return total + triangle[row][column]
return max(golden_pyramid(triangle, row + 1, column, total + triangle[row][column]),
golden_pyramid(triangle, row + 1, column + 1, total + triangle[row][column]))
Как мы видим, на первом уровне мы запустим нашу функцию два раза, затем 4, 8, 16 раз и так далее. В итоге мы получим сложность алгоритма 2N и, например, для 100-уровневой пирамиды нам нужно будет уже где-то ≈1030 вызовов функции. Многовато.
Динамическое программирование
Что если попробовать использовать принцип динамического программирования и разбить нашу проблему на множество мелких подзадач, результаты которых мы затем аккумулируем. Попробуйте взглянуть на треугольник вверх ногами. А теперь на второй уровень (то есть предпоследний от основания). Для каждой ячейки мы можем решить, каким будет лучший выбор в наших маленьких трёхэлементных треугольничках. Выбираем лучший, суммируем с рассматриваемой ячейкой и записываем результат. Таким образом, мы получили наш треугольник, но на один уровень ниже. Повторяем данную операцию снова и снова. В результате нам нужно (N-1)+(N-2)+…2+1 операций и сложность алгоритма равна N2.
def golden_pyramid_d(triangle):
tr = [row[:] for row in triangle] # copy
for i in range(len(tr) - 2, -1, -1):
for j in range(i + 1):
tr[i][j] += max(tr[i + 1][j], tr[i + 1][j + 1])
return tr[0][0]
Решения игроков CheckiO
Пользователь gyahun_dash написал интересную реализацию описанного выше метода ДП в своем решении «DP». Он использовал reduce, чтобы проходить по парам строк, и map чтобы обработать каждую из них.
from functools import reduce
def sum_triangle(top, left, right):
return top + max(left, right)
def integrate(lowerline, upperline):
return list(map(sum_triangle, upperline, lowerline, lowerline[1:]))
def count_gold(pyramid):
return reduce(integrate, reversed(pyramid)).pop()
Игрок evoynov использовал двоичные числа, чтобы перебрать все возможные маршруты, представленные как последовательность 1 и 0 в своем решении «Binaries». И это наглядный пример сложности алгоритма с рекурсией и перебором всех маршрутов.
def count_gold(p):
path = 1 << len(p) res = 0 while bin(path).count("1") != len(p) + 1: s = ind = 0 for row in range(len(p)): ind += 1 if row > 0 and bin(path)[3:][row] == "1" else 0
s += p[row][ind]
res = max(res, s)
path += 1
return res
И чтобы не было скучно, посмотрим на легкий мозгодробитель от пользователя nickie и его однострочник «Functional DP», который только формально состоит из двух строк. Конечно, это решение из категории «Творческих» («Creative»). Не думаю, что автор использует такое на боевом коде. А просто для так для веселья, почему бы и нет.
ount_gold=lambda p:__import__("functools").reduce(lambda D,r:[x+max(D[j],D[j+1])
for j,x in enumerate(r)],p[-2::-1],list(p[-1]))[0]
Задача №5.
Эта задача — вариант классического вопроса, задававшегося на собеседованиях в Microsoft, когда претендентов спрашивали, сколько раз в день часовая и минутная стрелки встречаются друг с другом. Поскольку этот вопрос сейчас стал широко известен, интервьюверы начали использовать его разновидность.
Рассмотрим сначала вариант наиболее ожидаемого решения, математического. Во-первых, представьте ситуацию, когда часовая и минутная стрелки наложились. Все знают, что это происходит в полночь, затем приблизительно в 1:05, 2:10, 3:15 и так далее. Другими словами, они накладываются друг на друга каждый час, за исключением периода от 11:00 до 12:00. В 11:00 более быстрая минутная стрелка находится на 12, а более медленная часовая — на 11:00. До 12:00 дня они друг с другом не встретятся, и поэтому их наложения в районе 11 часов не будет.
Таким образом, за каждый 12-часовой период происходит 11 наложений. Они равномерно распределены во времени, поскольку обе стрелки двигаются с постоянной скоростью. Это означает, что интервалы между наложениями составляют 12/11 часа. Это эквивалентно 1 часу 5 минутам 27 и 3/11 секундам. Поэтому за каждый 12-часовой цикл наложения происходят в периоды, указанные на картинке.
Вернёмся к секундной стрелке. Её наложение на минутную возможно тогда, когда число минут совпадает с числом секунд. Точное наложение происходит в 00:00:00. В целом минутные и секундные стрелки накладыватся лишь на долю секунды. Например, в 12:37:37 секундная стрелка будет показывать на 37, отставая от минутной, которая в это время будет между 37 и 38 и отставать от часовой. Через мгновение минутная и секундная наложатся, но часовой возле них не будет. Т.е. наложения всех трёх стрелок не произойдет.
Секундная стрелка не наложится ни в одном из вариантов на картинке, за исключением полуночи и полудня. Это означает, что финальный ответ на вопрос: дважды в сутки.
А вот ответ, приветствуемый в Google. Секундная стрелка предназначена для показа коротких временных интервалов, а не для сообщения времени с точностью до секунды. Если она не синхронизирована с двумя другими стрелками, это вполне нормально. Под «синхронизацией» здесь понимается, что в полночь и полдень все три стрелки указывают точно на 12. Большинство аналоговых часов всех видов не позволяют вам точно установить секундную стрелку. Нужно было бы извлечь батарейку или подождать, если говорить о механических часах, когда закончится завод пружины, а затем, когда секундная стрелка остановлена, синхронизировать минутную и часовую стрелки друг с другом, после чего дождаться, когда наступит время, показанное на часах, чтобы вернуть батарейку или завести часы.
Чтобы все это проделать, нужно быть маньяком или фанатеть от пунктуальности. Но если вы всего этого не проделаете, секундная стрелка не будет показывать «реального» времени. Она будет отличаться от точных секунд на какую-то величину в случайном интервале, доходящем до 60 секунд. Учитывая случайные расхождения, шансов на то, что все три стрелки когда-либо встретятся, не существует. Этого не случается никогда.
Задача №6.
Вы играете в футбол на пустынном острове и хотите подбросить монетку, чтобы решить, какой команде достанется мяч. Единственная монета, что у вас есть, является гнутой, и поэтому вносит явные искажения в результат при подбрасывании. Как вы тем не менее можете использовать такую монету, чтобы принять справедливое решение?
Есть два варианта решения этой задачи.
Первый состоит в том, чтобы подбрасывать монету множество раз, чтобы определить процент выпадания орла и решки. После того как вы установите, например, что монета выпадает орлом в 54.7% случаев (с установленным пределом ошибки), вы используете этот факт, чтобы продумать ставку со множеством подбрасываний, при котором шансы на получение результата будут близки к желаемому.
Второй ответ куда проще: подбросьте монету дважды. Возможны четыре исхода: ОО, ОР, РО и РР (Р — решка, О — орёл). Поскольку монета «благосклонна» к одной стороне, шансы выпадения ОО не эквивалентны шансам РР. С другой стороны, вероятности выпадения ОР и РО должны быть одинаковы, независимо от степени «благосклонности» монеты. Одна команда ставит на ОР, вторая — на РО. Если выпадает ОО или РР, игнорируйте их результаты и бросайте еще два раза.
Помимо того, что эта схема проще, она к тому же и, бесспорно, справедлива. Первый же вариант, если говорить о точности, лишь приближается к шансам пятьдесят на пятьдесят.
Задача №7.
Это вопрос труден только потому, что та информация, которую вы получили, не является той, которую вы хотели бы иметь. Однако в реальной жизни такое часто встречается.
Вы хотели бы определить вероятность, относящуюся к 10 минутам, имея вероятность для 30 минут. Вы не можете поступить просто, то есть разделить 0.95 на три (хотя надо сказать, что некоторые пытаются это сделать). Не очень помогает знание вероятности того, то автомобиль проедет в течение 30 минут, поскольку это может случиться в любое время. Автомобиль может проехать в первый 10-минутный отрезок или во второй, или в третий. За каждый из этих периодов могут проехать два автомобиля или пять, или тысяча, но это все считается как проезд автомобиля.
То, что вы хотели бы на самом деле знать, — это вероятность того, что за 30-минутный период не проедет ни один автомобиль. Узнать ее довольно просто. Поскольку имеется шанс, равный 95%, что за 30 минут проедет по крайней мере один автомобиль, то вероятность того, что в течение этого временного промежутка не будет ни одной машины, должна быть равна 0.05.
Чтобы в течение 30-минутного отрезка не было ни одного автомобиля, должны случиться (или, наоборот, не случиться) три вещи. Во-первых, в течение 10 минут не должно быть ни одного автомобиля. Затем должно пройти еще 10 минут без всяких машин. И, наконец, третьи 10 минут также должны быть без автомобилей. В вопросе спрашивается вероятность появления автомобиля в течение 10-минутного периода. Назовем ее X. Вероятность отсутствия машин в эти 10 минут равна 1 - X. Умножим эту величину саму на себя три раза. Она должна быть равна 0.05, то есть
(1 - X)³ = 0.05
Извлечем кубический корень из обеих частей.
1 - X = ³Ѵ0.05
Решим это уравнение относительно X.
X = 1 - ³Ѵ0.05
Никто не ожидает, что вы можете в уме извлекать кубические корни. Компьютер вам подскажет, что ответ равен около 0.63. Такой результат вполне обоснован. Вероятность появления автомобиля в 10-минутный период должна быть меньше, чем вероятность его появления, равная 0.95, за 30-минутный период.
Задача №8.
Не все понимают сразу о чем речь: территориально это место, где нет никаких заправочных станций. Единственное место, где можно здесь найти горючее – это топливные баки грузовиков. Пересесть из грузовика в гибридный легковой автомобиль Prius нельзя. Бросить грузовик без топлива, где бы это ни случилось, и без водителя – в порядке вещей. И единственное, что здесь важно, – доставить как можно дальше ценный груз.
Топлива хватит, чтобы отправить каждый из 50-ти грузовиков на расстояние 100 км, то есть на расстояние 50*100 = 5000 км. Но возможно ли считать 5000 км ответом? Нет, если только у вас нет способа, позволяющего телепортировать топливо из бака одного грузовика в другой. Вспомните, что каждый грузовик полностью заправлен и пока топливо не израсходовано, добавить его нельзя.
Начните с простого шага. Представьте, что у вас не 50 грузовиков, а всего один. Загружайте его, залезайте в кабину и отправляйтесь в путь. Через 100 км путь для вас закончится.
Теперь предположим, что у вас есть два грузовика. Загружаете первый и 100 км можете ни о чем не думать. Но потом? Сможет ли вам помочь второй грузовик? Нет. Он на расстоянии 100 км от вас. Ему придется следовать за вами, так что его бак закончится через те же 100 км.
Может быть, первому грузовику следовало бы взять второй на буксир? Когда первый грузовик останется без топлива, можно переложить груз во второй грузовик, бак которого полон, и двигаться дальше. Да, хорошо, еще 100 км.
И насколько далеко в такой сцепке сможет проехать первый грузовик? Вряд ли 100 км. Ему придется тащить вес вдвое больше обычного. Законы физики говорят, что в лучшем случае он проедет только половину прежнего расстояния. В реальной жизни расход топлива на 1 км пути для более тяжелого транспортного средства повышается более резко, чем вес.
А если посмотреть иначе? Пусть два грузовика отправляются в путь одновременно, каждый сам по себе. Через 50 км баки у каждого будут наполовину пустые, но один бак вы можете заполнить доверху. Перелейте топливо из одного бака в другой. Оставьте пустой грузовик и проезжайте на заполненном доверху баке еще 100 км. Пройденное суммарное расстояние составит 150 км. В отличие от буксировки, здесь нет теоретического ограничения, и такой подход в полной мере может быть использован на практике.
При трех грузовиках вариант с буксировкой ставится под сомнение, а вот идея с переливанием топлива по-прежнему работает отлично. Отправьте сразу три грузовика. Пусть они остановятся на трети пути расстояния в 100 км, то есть после того, как проедут примерно 33.33 км. В каждом баке осталось 2/3 топлива. Перелейте топливо из одного грузовика в баки двух других – они снова полны доверху. Затем отправьте в путь эти два грузовика. Мы уже знаем, что максимальное расстояние для них составит 150 км. Если добавить к этому пути первые 33.33 км, то общее расстояние будет чуть больше 183 км.
Закономерность становится очевидной. Один грузовик может проехать 100 км. Второй грузовик позволяет увеличить общий путь на 100/2 = 50 км. Третий грузовик увеличивает общий путь на 100/3 км. Четвертый грузовик добавляет 100/4 км. Для N грузовиков общее расстояние составит: 100*(1/1+1/2+1/3+1/4+1/5+…1/N)
Дробная часть в этом случае известна как гармонический ряд. Сумму членов гармонического ряда можно легко рассчитать. Если N равно 50, сумма этой прогрессии 4.499… Умножьте ее на 100 км, и вы увидите, что, имея в своем распоряжении 50 грузовиков, вы сможете доставить груз на 449.9 км.
При увеличении N сумма возрастает. При достаточном количестве грузовиков вы можете отвезти груз куда захотите. Однако с увеличением N расстояние увеличивается очень медленно, а эффективность использования энергии становится очень низкой. Тысячный грузовик добавит лишь 1/100 км к общему расстоянию перевозки груза (но при этом загрязнит атмосферу выбросами диоксида углерода точно так же, как и все остальные машины). Миллионный грузовик увеличит весь путь всего на несколько сантиметров.
Приведенный выше ответ имеет право на жизнь. Есть ли другой? Есть, если можно перевозить топливо, и если груз не очень тяжелый.
В вопросе говорится о грузовиках, которые предназначены для перевозок крупных и тяжелых грузов. Предположим, у вас грузовики марки GMC или Ford. Собственный вес такого полностью заправленного и оборудованного автомобиля – порядка 2250 кг. Он сконструирован так, чтобы безопасно перевозить такой тяжелый груз, если только вы не транспортируете упакованный арахис или сахарную «вату».
Бак грузовика вмещает около 30 галлонов топлива, этот объем эквивалентен примерно 120 литрам.
Ключевой вопрос: весит ли топливо меньше, чем сам грузовик? Меньше, поскольку 200/5000 составляет 1/25 веса грузовика без груза, но заправленного.
Было бы глупо буксировать или везти грузовик весом 2250 кг, когда вас интересует только 120 литров топлива в его баке. Не лучше ли везти топливо в кузове грузовика вместе с доставляемым грузом. (Может быть, вы сможете найти емкости для топлива или снять топливные баки с других грузовиков и использовать их как такие емкости.) Грузовик может перевезти топливо, эквивалентное полной заправке 25 грузовиков при условии, что полезный груз весит немного.
Это означает, что один такой грузовик может перевезти половину топлива парка, состоящего из 50 машин. Он может проехать 25*100 или 2500 км. Однако, вряд ли он это сделает, потому что перевозимый груз сократит это расстояние. Тем не менее, будем считать, что такой вариант позволит ему проехать порядка 1500 км. Это более чем в три раза превышает 450 км при варианте перелива топлива и требует всего лишь одного грузовика и одного водителя.
Задача №9.
Этот вопрос задавали ранее в Apple. Большинство людей понимают, что при его анализе необходимо учесть центробежную силу. В равной степени вам нужно знать и силу трения. Оно возникает между дном стакана и вращающимся диском, который приводит стакан в движение.
Чтобы сделать ситуацию более понятной, представьте мир, где трение вообще отсутствует. Каждая вещь становится более скользкой, чем тефлон, причем более скользкой бесконечно. Тогда в эксперименте, описанном в вопросе, не будет никакого влияния на стакан. Диск проигрывателя будет вращаться под стаканом, не оказывая на него никакого влияния, то есть стакан вообще не будет двигаться. Это верно в соответствии с первым законом Ньютона: неподвижные объекты остаются в этом положении до тех пор, пока на них не воздействует какая-то сила. Без силы трения стакан не будет перемещаться.
Теперь представьте противоположный вариант: стакан при помощи очень прочного клея Krazy Glue приклеили к диску, и между двумя поверхностями появилась практически бесконечно высокая сила трения. Стакан и диск в этом случае будут вращаться как единое целое. Увеличьте скорость диска, и стакан будет вращаться быстрее. Это приведет к увеличению центробежной силы. Единственное, что сможет в этих условиях свободно реагировать на эту силу, будет вода. Ведь она-то ко дну стакана не приклеена. Когда стакан будет крутиться с достаточно большой скоростью, вода прольется в сторону, противоположную центру вращения.
В вопросе вас просят рассмотреть вариант, лежащий между предельными ситуациями. Вначале трение будет достаточным, чтобы удерживать стакан на месте. Он будет вращаться вместе с диском, создавая небольшую центробежную силу. По мере увеличения скорости вращения, центробежная сила будет возрастать. Давление, удерживающее стакан на месте, будет оставаться примерно одинаковым. Поэтому должен наступить какой-то момент, когда центробежная сила превысит силу давления.
Те, кто изучал физику или проводил много времени в детских играх, вспомнят, что когда предмет начинает скользить, сила трения становится меньше, чем когда он стоит. На верхней части ледяной горки вы немного «прилипаете», но затем неожиданно начинаете свободно по ней двигаться вниз. То же самое относится и к диску. Вместо того, чтобы все время ускоряться постепенно, стакан вначале удерживается, и только через какое-то время начинает двигаться.
Что случится потом? Ответ здесь таков: это зависит от формы стакана и от того, насколько он заполнен водой. Однако если вы ограничитесь только этим ответом, интервьюер может решить, что вы пытаетесь уйти от вопроса. Вот варианты, которые возможны в реальной жизни.
1. Заполните стакан водой до краев. Даже самая небольшая центробежная сила приведет к повышению уровня воды над внешним краем стакана. Из-за чего часть воды прольется. Это случится даже тогда, когда стакан «приклеен», то есть до того, как он начнет скользить.
2. Используйте очень низкий стакан, к примеру, чашку Петри с каплей воды в ней. Если вы выбрали такой сосуд для эксперимента, он не перевернется и не будет двигаться настолько быстро, что единственная капля воды поднимется по его стенке и прольется. Зато чашка Петри с этой каплей просто соскользнет с диска.
3. Используйте очень высокий стакан, вроде пробирки с плоским днищем. Центробежная сила фактически действует на центр тяжести. Поскольку центр тяжести в данном случае расположен высоко, а вся сила трения прикладывается в самом низу, стеклянная пробирка скорее опрокинется, чем будет скользить.
Важно учесть и поверхность диска. Если она изготовлена из резины, это повысит трение и с большей вероятностью приведет к выплескиванию и опрокидыванию, здесь они в равной мере вероятны. Более скользкая твердая пластиковая поверхность способствует реализации варианта скольжения.
Задача №10.
Эта головоломка в своё время была популярна в JP Morgan Chase. Понятное дело, оказавшись в темноте, вы просто достанете сотовый телефон и воспользуетесь экраном как фонариком. Однако эта задачка появилась до эпохи сотовых телефонов, и её можно решить, даже не видя карт. Вполне вероятно, вы начнете со следующих наблюдений.
• При произвольном делении колоды вряд ли в каждой стопке окажется равное количество карт рубашками вверх (такое возможно, только если вам улыбнулась удача). Более того, все карты, лежащие рубашкой вверх, могут оказаться в одной стопке.
• В вопросе не говорится, что обе стопки должны быть равными, а только о том, что в них должно быть одинаковое количество карт рубашками вверх.
• Вы можете переворачивать карты. Конечно, у вас нет способа, подсказывающего вам, переворачиваете вы карты рубашкой вверх или вниз.
Ожидаемый ответ заключается в том, что вы должны отсчитать N карт, начиная с верха колоды, и перевернуть их. Это будет одна стопка. Оставшаяся часть колоды составит вторую стопку.
Объясним, почему это работает. В N картах, которые вы отсчитали, может быть любое число карт, лежащих рубашкой вверх, от нуля до N. Представим, что там было (до переворачивания) f таких карт. Перевернув карты, вы добились, что каждая карта рубашкой вверх становится картой рубашкой вниз и наоборот. Поэтому вместо f карт рубашкой вверх вы приходите к варианту N-f карт рубашкой вверх в этой стопке.
В другой стопке, в которой содержится остаток колоды, имеется N карт, лежащих рубашкой вверх, за минусом тех f, которые вы отсчитали. Это то же самое количество, как в первой стопке с перевернутыми картами.
Задача №11.
На острове существует правило — голубоглазые люди не могут там находиться. Самолет улетает с острова каждый вечер в 20:00. Все жители собираются за круглым столом ежедневно, каждый человек может видеть цвет глаз других людей, но не знает цвет собственных. Никто не имеет права сказать человеку, какой у его цвет глаз. На острове находится не менее одного голубоглазого человека. Сколько дней потребуется, чтобы все голубоглазые уехали?
Решение
Давайте используем подходы «базовый случай» и «сборка». Предположим, что на острове находится N голубоглазых людей. Мы знаем, что N > 0.
N = 1: у одного человека голубые глаза
Предположим, что все люди на острове достаточно умны. Если известно, что на острове есть только один голубоглазый человек, то, обнаружив, что у всех глаза не голубые, он придет к выводу, что он и является тем единственным голубоглазым человеком, которому следует улететь вечерним рейсом.
N = 2: у двух человек голубые глаза
Два человека с голубыми глазами видят друг друга, но не знают, чему равно c: c = 1 или c = 2. Из предыдущего случая известно, что если c = 1, то голубоглазый человек может себя идентифицировать и покинуть остров в первый же вечер. Если голубоглазый человек находится на острове (c = 2), это означает, что человек, видящий только одного голубоглазого, сам голубоглаз. Оба человека должны будут вечером покинуть остров.
N > 2: общий случай
Давайте использовать ту же логику. Если N = 3, то эти три человека сразу увидят, что на острове есть еще 2 (или 3) человека с голубыми глазами. Если бы таких людей было двое, они покинули бы остров накануне. Поскольку на острове все еще остаются голубоглазые люди, то любой человек может прийти к заключению, что c = 3 и что у него голубые глаза. Все они уедут той же ночью.
Такой шаблон можно использовать для произвольного значения N — если на острове находится N человек с голубыми глазами, понадобится N ночей, чтобы все они покинули остров.
Задача №12.
Напишите метод, тасующий карточную колоду. Колода должна быть идеально перемешана. Перестановки карт должны быть равновероятными. Вы можете использовать идеальный генератор случайных чисел.
Решение
Это очень популярная задача и известный алгоритм. Если вы еще не знакомы с решением, читайте дальше.
Давайте будем решать задачу «в лоб». Можно выбрать карты в произвольном порядке и поместить их в новую колоду. Фактически колода представляет собой массив, следовательно, нам нужен способ, позволяющий заблокировать отдельные элементы.
Исходная колода (до выбора 4): [1] [2] [3] [4] [5]
/* Выбираем случайный элемент для помещения его в начало перетасованной колоды
* Помечаем элемент в оригинальной колоде как "заблокированный", чтобы
* не выбрать его снова */
Перемешанная колода (после выбора 4): [4] [?] [?] [?] [?]
Исходная колода (после выбора 4): [1] [2] [3] [X] [5]
Если мы пометим элемент [4], что помешает выбрать его еще раз? Один из способов – поменять местами «мертвый» ([4]) и первый элементы колоды:
Исходная колода (до выбора 4): [1] [2] [3] [4] [5]
/* Выбираем случайный элемент для перемещения его в начало перетассованной колоды
* Существует элемент 1, который заменит выбранный элемент. */
Перемешанная колода (после выбора 4): [4] [?] [?] [?] [?]
Исходная колода (после выбора 4): [X] [2] [3] [1] [5]
/* Выбираем случайный элемент для перемещения его в начало
* перетасованной колоды. Есть элемент 2, который заменит только что
* выбранный элемент */
Перетасованная колода (после выбора 3): [4] [3] [?] [?] [?]
Исходная колода (после выбора 3): [X] [X] [2] [1] [5]
Алгоритм проще реализовать для ситуации, когда «мертвы» первые k карт, чем для ситуации, когда, например, «мертвы» третья, четвертая и девятая карты.
Оптимизировать алгоритм можно, объединив перемешанную и исходную колоды вместе.
Исходная колода (до выбора 4): [1] [2] [3] [4] [5]
/*Выбираем случайный элемент между 1 и 5 и меняем его местами с 1.
* В этом примере мы выбрали элемент 4.
* После этого элемент 1 - "мертв" */
Исходная колода (после выбора 4): [4] [2] [3] [1] [5]
/* Элемент 1 "мертв". Выбираем случайный элемент для замены с
* элементом2. В этом примере пусть мы выберем элемент
* 3.*/
Исходная колода (после выбора 3): [4] [3] [2] [1] [5]
/* Повторяем. Для всех i между 0 и n-1 меняем местами случайный элемент j
* (j >= i, j < n) и элемент i. */
Этот алгоритм легко реализовать итеративно:
public void shuffleArray(int[] cards) {
int temp, index;
for (int i = 0; < cards.length; i++) {
/*Карты с индексами от 0 до i-1 уже были выбраны
* (они перемещены в начало массива), поэтому сейчас мы
* выбираем случайную карту с индексом, больше или равным i
* */
index = (int) (Math.random() * (cards.length - i)) + i;
temp = cards[i];
cards[i] = cards[index];
cards[index] = temp;
}
}
Подобный алгоритм можно придумать и самостоятельно, он достаточно часто встречается на собеседовании. Перед интервью стоит убедиться, что вы понимаете механизм его работы.
Задача №13.
У вас есть стеклянный кувшин, в котором лежат небольшие шарики, и вы в любое время можете определить их количество. Вы со своим другом играете в следующую игру: каждый из вас по очереди забирает из кувшина 1 или 2 шарика. Игрок, который забирает последний шарик, выигрывает. Какая самая лучшая стратегия в этой игре? Можете ли вы в самом начале предсказать, кто выиграет?
Число шариков становится все меньше и меньше с каждым ходом, и, в конце концов, их станет как-то совсем мало. Вот тут-то стратегия становится совершенно понятной.
Давайте исходить из того, что в кувшине остался всего один шарик и теперь моя очередь брать. Взяв последний шарик, я выиграю.
Я выиграю и при двух оставшихся шариках, потому что могу взять оба.
Но три оставшихся шарика для меня плохой вариант. Мне придется оставить либо один, либо два шарика, и тут-то мой соперник немедленно воспользуется таким подарком.
Четыре и пять шариков — хороший вариант. Я могу оставить моего соперника с неудачным (уже для него) числом три.
Ну что ж, все понятно. Число, которое делится на три, означает для меня проигрыш: 3, 6, 9, 12… — плохие варианты, когда моя очередь ходить. Все другое (1, 2, 4, 5, 7, 8…) — прекрасно.
Так как теперь этим воспользоваться в игре? Мы начинаем с большого, но неизвестного числа шариков. Разделим его на 3. Если число делится без остатка, это неудачный для нас вариант. Тогда постарайтесь не ходить первым. Если соперник предложит вам бросить монетку, чтобы решить, кто должен ходить первым, проявите «великодушие» и позвольте ему сделать первый ход. Если же вам улыбнулась удача и число шариков не делится на три, и вы ходите первым, то стратегия выигрыша проста: с каждым ходом берите столько шариков, чтобы в кувшине оставалось проигрышное число. Скажем, если вы начнете с 304 шариков (прекрасно для вас), вы забираете один, оставляя сопернику неудачные для него 303. Поступайте так при каждом ходе, и, в конце концов, он останется с тремя шариками. Такая стратегия обеспечит вам победу.
Более того, такая стратегия совершенно надежно приведет вас к выигрышу, независимо от того, как будет действовать другой игрок (если только в порыве гнева он не размахнется кувшином об пол). Ему приходится забирать один или два шарика из оставшегося числа, неудачного для него. Это всегда позволяет вам при следующем ходе оставлять в кувшине «удачное» число шариков.
Но что делать, если вы начинаете с неудачного расклада? Вы обречены на поражение, если другой игрок сам применит описанную выше стратегию. Однако пока никакой трагедии нет. Ваш соперник может и не знать о такой стратегии, а может просто просчитаться. Любой, кто играет без стратегии, почти обязательно рано или поздно предоставит вам возможность перейти к счастливому (для вас) числу, поскольку две трети всех чисел для вас выигрышны. Человек, который знает оптимальную стратегию, но в ходе игры ошибется хотя бы раз, обречен: он больше не командует парадом (конечно, при условии, что вы такой ошибки не совершите).
Но, собственно, вас-то спрашивают, можно ли предсказать, кто выиграет. Да, если оба игрока идеально знают теорию этой игры. Определите, является ли первоначальное число шариков «счастливым». Если да, то первый игрок всегда выиграет. И наоборот.
Но живем мы с вами в реальном мире. Кто возьмется предсказать конечный результат?! Даже если оба игрока знают правильную стратегию, чем больше шариков в игре, тем выше вероятность ошибки. Шансы выше у того, кто не ошибется, следуя выигрышной стратегии.
Встречаются и варианты этого вопроса, например такой: проигрывает тот, кто забирает последний шарик. Как поступить в этом случае? «Неудачное» число шариков запишем в виде 3N+1, а затем будем применять ту же самую стратегию.
Задача №14.
Вы не можете пользоваться секундомером. В каждом заезде могут участвовать только пять лошадей.
Вы можете начать свой ответ с уточнения: спросите интервьюера, следует ли считать «самой быстрой лошадью» ту, которая выигрывает конкретную скачку. Хотя этот вариант не работает на ипподроме, он в значительной степени упрощает задачу: предположим, что если А побеждает В в одной гонке, то А объективно и бесспорно более быстрая лошадь, чем В. Если вам скажут, что использовать это допущение можно, то в отдельной гонке действительно победит самая быстрая лошадь.
Первое, что приходит в голову, — нужны, по крайней мере, пять забегов. Любая из лошадей может быть в числе первых трех. К тому же вам потребуется устроить забеги для всех 25 лошадей. Пять забегов по пять лошадей в каждом — никак иначе.
Логично. Второй вывод: пяти забегов недостаточно. Разделите 25 лошадей на группы по пять, и устройте забеги. В каждом забеге одна лошадь будет конкурировать с другими четырьмя. Скажем, в одной из гонок будут участвовать лошади, которые придут к финишу в следующем порядке.
1. Ридонна
2. Бавкида
3. Харцея
4. Вероника
5. Альмадена
Хотя в этом забеге победила Ридонна, по его результатам вы не можете прийти к выводу, что она является самой быстрой лошадью из 25 или даже входит в тройку сильнейших. Чтобы пояснить последнее утверждение, воспользуемся крайним случаем: представим, что все самые медленные лошади в других заездах являются более быстрыми, чем Ридонна (которая, возможно, в общем рейтинге займет лишь 21-е место из 25 возможных).
Узнали ли мы что-нибудь из этого заезда? Разумеется, да. Мы узнали, как проранжировать пять конкретных лошадей. Мы также узнали, что можем вычеркнуть из числа претенденток на число лучших Веронику и Альмадену. Поскольку они не вошли в тройку первых в этом заезде, они не могут быть и в тройке самих быстрых из 25 лошадей.
То же самое можно сказать о лошадях, занявших четвертое и пятое места в других забегах. В каждом забеге из пяти лошадей две выбывают из дальнейшего рассмотрения. После первых пяти забегов мы можем вычеркнуть 10 лошадей, оставив 15 в качестве претендентов на звание самих быстрых трех.
Шестая гонка должна сравнить лошадей, которые хорошо показали себя в первых пяти заездах. Кажется разумным устроить гонки для победителей первых пяти заездов. Давайте так и сделаем. Возьмем Ридонну из заезда, описанного выше, и отправим ее на соревнования с победителями других заездов. Конечный результат может выглядеть следующим образом.
1. Фидана
2. Ридонна
3. Флавия
4. Принцесса Гита
5. Сикарель
Опять же мы можем обоснованно вычеркнуть из числа претендентов на победу Принцессу Гиту и Сикарель. Они, очевидно, если руководствоваться результатами этого забега, не могут входить в число трех быстрейших из 25. Мы также узнаем, что самой быстрой лошадью является Фидана, поскольку она опередила всех остальных лошадей, которые были первыми в предыдущих забегах. Если вопрос заключался бы в том, чтобы определить самую быструю лошадь из 25, то мы уже получили бы ответ. Ею является Фидана.
Однако нам надо определить трех самых быстрых. Из числа претенденток на победу мы можем вычеркнуть не только Принцессу Гиту и Сикарель, но и всех тех лошадей, которых они опередили в первых скачках. Лошади, которых они опередили, были более медленными, а мы уже знаем, что победители двух забегов из списка вычеркнуты.
Теперь давайте разберемся с Флавией. Поскольку она пришла третьей в этом забеге, все лошади, которых она опередила в первом забеге, также исключаются из дальнейшего рассмотрения.
Теперь перейдем к Ридонне. Исходя из последней гонки, она, возможно, в лучшем случае является второй лошадью из всех. Это оставляет открытым вопрос о Бавкиде. которая в первом круге пришла второй, после Ридонны, но в целом она может быть третьей из всех лошадей. (В этом случае список победителей был бы таким: Фидана, Ридонна, Бавкида).
Харцея, пришедшая третьей в первой гонке, где победителем была Ридонна, теперь выбывает из дальнейшего участия.
Две лошади, пришедшие второй и третьей после Фиданы в первой гонке, все еще остаются претендентами. Возможно, эти лошади быстрее Ридонны. но они никогда с ней не соревновались.
Итак, осталось шесть лошадей. Из них три были первыми в последней гонке: две, которые пришли второй и третьей в гонке с общим победителем, и одна, которая пришла второй в своей первой гонке, уступив только лошади, которая в общем зачете заняла второе место.
Мы уже знаем, что самая быстрая из всех лошадей — Фидана. По этой причине нет смысла опять устраивать с ней гонки. Остается всего пять лошадей. Естественно, мы устроим забег для них в седьмом и последнем раунде. Первые две лошади, оказавшиеся здесь победителями, в итоге займут второе и третье места.
Небольшое изменение правил. Начните с квалификационного раунда из пяти забегов, в которых будут соревноваться все 25 лошадей. Затем выберите вариант чемпионской гонки: в следующий круг будут допущены только победители квалификационных заездов. Лошадь, которая придет первой во второй гонке, и станет общим победителем.
Задача №15.
Не все любители чая положительно относятся к кофе; не все любители котов терпят собак, и не все фанаты одной команды одновременно являются болельщиками другой. Нарисуйте диаграмму Венна на доске или хотя бы мысленно. Она представляет собой прямоугольник, чья площадь соответствует числу участников исследования. Пусть большая часть этого прямоугольника соответствует 70% — это число респондентов, любящих кофе, а небольшой кружок внутри отражает 30% тех людей, которые, очевидно, не любят кофе. (Общая площадь всего прямоугольника должна составлять 100%, хотя добиваться такой точности на картинке не обязательно.)
80% респондентов любят чай. Если эти проценты показать в виде круга, то он наложится на те части, которые отражают любителей кофе, и тех, кто негативно относится к этому напитку. (Группа любителей кофе просто недостаточна, чтобы вобрать в себя всех тех, кто любит чай.) Чтобы задать верхнюю границу людей, любящих оба напитка, предположим, что каждый любитель кофе любит и чай.
Поэтому круг, отражающий 80% любителей чая, можно разделить на две части: тех, кто любит и чай, и кофе (70%) и тех, кто любит только чай (10%). 70% являются верхней границей.
Чтобы получить нижнюю границу, сместим круг, относящийся к любителям чая, так, чтобы он закрыл круг тех, кто не любит кофе. Теперь каждый, кому не нравится кофе (30%), любит чай. Это приводит к 80 – 30 = 50% тех, кто любит чай и кофе. Эта цифра является нижней границей.
Задача №16.
В этот бар ходят необщительные посетители. Вдоль барной стойки расположены 25 мест. Всякий раз, когда входит новый посетитель, он обязательно садится на самое дальнее, насколько это возможно, место от остальных гостей. Ни один не сядет рядом с кем-то другим: если посетитель входит и видит, что «свободных» мест нет, он тут же разворачивается и уходит из бара. Бармену, естественно, хочется, чтобы за стойкой сидело как можно больше клиентов. Если ему разрешено усадить первого посетителя на любое место, куда выгоднее его посадить с точки зрения бармена?
Самый плотный из возможных вариантов — чередование клиентов и пустых мест, при котором оба крайних места заняты. Это позволило бы остальным посетителям сесть на все места с нечетными номерами, в том числе и крайние под номерами 1 и 25, и оставить все четные номера пустыми. В этом случае у стойки могло бы разместиться 13 клиентов.
Однако такое размещение не всегда работает. Предположим, первый клиент уселся на место № 1. Следующий «отшельник» выбирает место под номером № 25, поскольку оно располагается на самом далеком из всех возможных расстояний от № 1 Третьему клиенту придется сесть в середину барной стойки, на место № 13. Два следующих посетителя заполнят пустоты и усядутся соответственно на места № 7 и № 19. Пока все хорошо.
В конце концов, кто–то захочет сесть между клиентами, занимающими места № 1 и № 7. Он выберет № 4, поскольку это позволит ему иметь два пустых сиденья между собой и ближайшими соседями. Но ни один из следующих гостей не сядет рядом с ним. Остальная часть барной стойки заполнится точно так же, и поэтому между двумя посетителями будут пустоты в два места, что делает эту схему минимально эффективной из возможных (при ней у стойки окажутся лишь девять клиентов вместо оптимального числа — 13).
Многие задачи, в том числе и эту, лучше всего решать, двигаясь от конца к началу. Мы знаем, каким должен быть желательный для нас план рассадки, и надо определить, как на него выйти.
Как показано на диаграмме, для этой схемы характерна большая симметрия, напоминающая рост кристалла. Небольшие части барной стойки заполняются как раз таким образом. Обратите внимание на ту часть стойки, в которой идут первые номера. Нужно, чтобы посетители заняли места № 1 и № 5, так как это позволит другому клиенту усесться на № 3.
Как вам добиться, чтобы пришедший в бар человек сел на место № 5? Ответ: надо, чтобы клиенты уже сидели на местах № 1 и № 9. Тогда пятое место будет посредине между ними, поскольку оно занимает максимальное расстояние и от № 1, и от № 9.
Как добиться, чтобы человек сел на № 9? Для этого предыдущие клиенты должны занять № 1 и № 17. А как сделать так, чтобы посетитель отправился на № 17? Скажем так, барная стойка недостаточно длинная, чтобы посадить клиентов на места № 1 и № 33. Поэтому бармену придется поступить просто — попросить первого посетителя сесть за № 17. Вот ответ.
Давайте отмотаем пленку назад. Первый клиент усаживается на № 17 (верхняя строка в диаграмме). Второй посетитель усаживается от него как можно дальше, на место № 1.
У третьего посетителя два варианта выбора: место № 9 пли № 25. Оба находятся на расстоянии семи пустых мест от любого другого клиента. Если исходить из замкнутого характера посетителей этого бара, третий клиент выберет скорее всего место № 25, поскольку в этом случае у него на расстоянии будет всего один сосед, а не двое, между которыми ему придется сидеть, и поэтому № 9 остается для четвертого клиента.
Следующие три посетителя выберут места между первыми четырьмя и займут соответственно места № 5, № 13 и № 21. На каждом из этих мест до ближайшего соседа их будет разделять три пустых сиденья.
И наконец, следующие шесть посетителей займут шесть оставшихся мест, у которых нет ближайших соседей, а именно: № 3, № 7, № 11, № 15, № 19 и № 23.
Бармен с таким же успехом мог бы попросить первого посетителя сесть на место № 9, и в этом случае диаграмма стала бы зеркальным отображением той, которая представлена выше.
Задача №17.
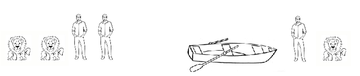
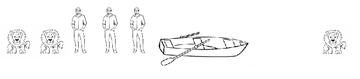
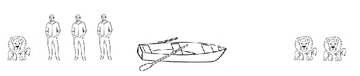
На одной стороне реки находятся три человека и три льва. Все они должны оказаться на другом берегу реки. Есть лишь одна лодка, в которой могут поместиться лишь два живых существа одновременно (человека или льва). Вы не можете оставлять на том или другом берегу реки больше львов, чем людей, так как в этом случае животные съедят людей, оставшихся в меньшинстве. Как вы переправите всех через реку?
Решение
Есть пять возможных вариантов первой поездки: один человек, один лев, человек и лев, два человека, два льва.
Так как львы не могут грести, а лодка сама не поплывет, значит, это исключает варианты с одним и двумя львами. Один и два человека тоже исключается, так как на одном берегу львов станет больше. Поэтому для первой поездки остается только один вариант: в лодке окажутся человек и лев.
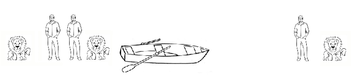
Они переправляются на дальний берег.
Но лодка сама вернуться не может. Из этого следует, что человек возвращается вместе с лодкой.
Рассмотрим варианты следующей поездки. Отправить двух людей мы не можем, иначе на берегу останется один человек и два льва. Поэтому единственным вариантом являются человек и лев. Человек отвозит льва на другой берег и тут же возвращается обратно. Поскольку в противном случае он останется на берегу с двумя львами.
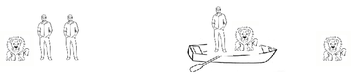
После этих двух поездок на дальнем берегу оказываются два льва, а на ближайшем берегу останутся три человека и один лев.
В следующей поездке у нас появляется возможность выбора. Мы можем отправить двух людей или человека вместе со львом. Если мы отправим человека и льва, то на дальнем берегу окажутся три льва, и безопасно перевести остальных людей уже не получится. Поэтому данный вариант отпадает.
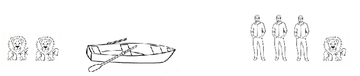
Вместо этого отправляем на другой берег двух людей, поскольку они по численности не уступают львам.
Но лодку надо вернуть обратно. Перевозить одного человека нельзя, поскольку на дальнем берегу останется человек и два льва. Поэтому обратно возвращаются человек и лев.
Теперь единственным разумным и безопасным вариантом является отправка двух человек на дальний берег.
Отправим обратно только одного человека. Он заберет льва (заманить его в лодку можно куском мяса) и вернется обратно.
Затем один человек возвращается за оставшимся львом.
И наконец, на дальний берег переплывают человек и лев.
ссылка на квест https://zen.yandex.ru/media/id/5ece9601 … 56401278bc
Отредактировано Ника (2020-06-15 18:40:07)